SLO - Suggestions for Locality Optimizations: Principles

Effectively using SLO to optimize a program's locality requires understanding the program and locality model used by SLO to analyze programs. Below, a short description of how data locality is modelled and on what basis SLO suggests refactorings is presented based on a running example.

1. Poor temporal locality is caused by data reuses that are far apart.

Basically, a cache can only improve execution time when data is reused. When reused data does not remain in the cache between the different uses, an opportunity exists to improve the cache behavior. Caches typically try to retain the most recently used data. Therefore, a datum is evicted from the cache between its reuses, when more data is accessed between those reuses than can fit in the cache.

Consider the following code:

The code produces the following trace of memory accesses at run-time, assuming len=4 and N=1:

There are 4 other elements accessed between the indicated reuses of Y[2]. Therefore, it is expected that the second access to Y[2] will be a cache hit, only when the cache can hold at least 5 elements.

2. Increasing temporal locality requires the reuses to be brought subtantially closer together.

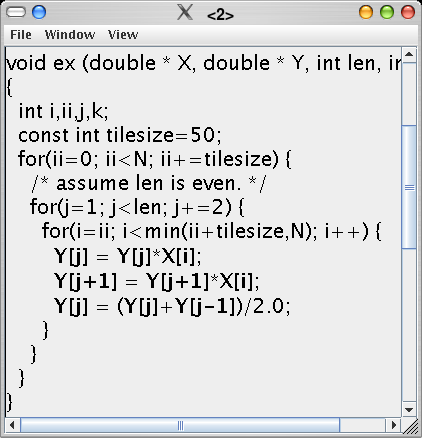
Therefore, increasing the temporal locality between the reuses requires dimishing the amount of data accessed between the cache-missing reuses. Typically, the amount of data accessed between reuses is much larger than the amount that can fit in the cache. Therefore, the amount of data between reuses needs to be reduced drastically.

Consider the same example code as above, but for more realistic values of len and N: len=100001 and N=10.

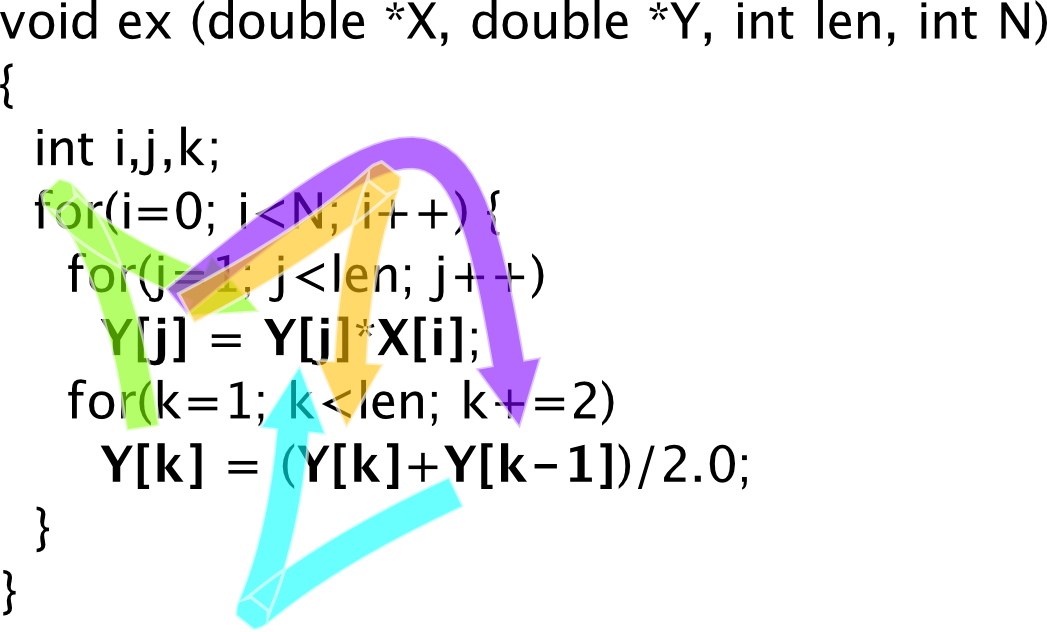
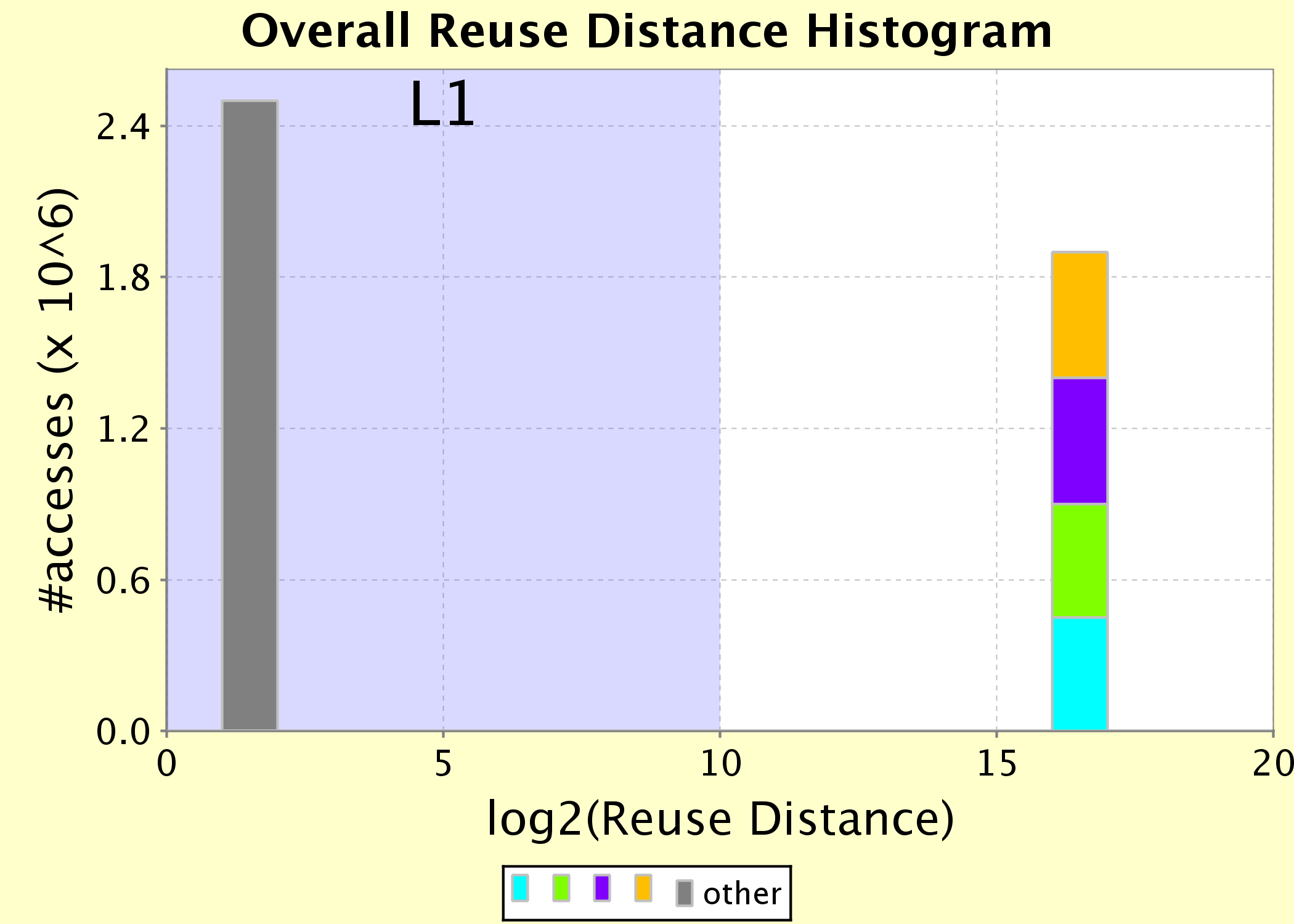
On the left, the array references that respectively produce the use and the subsequent reuse are indicated by arrows, which start at the use and point to the reuse. On the right, the distance between the corresponding reuses at run-time are shown in the histogram. Is shows that for the four arrows on the left hand side, the reuses have a distance between 2¹⁶ and 2¹⁷. In other words, between 2¹⁶ and 2¹⁷ other elements were accessed between the reuses. However, as indicated by the purple background, the L1 cache can only store 2¹⁰ elements. Therefore the reuses are not captured by the cache. In order to change these cache misses into hits, the number of elements between the reuses needs to be reduced to less than 2¹⁰. In other words, their reuse distance needs to be decreased by a factor of at least 2⁶=64. When len grows larger, the reuse distances will grow. However, assuming a fixed cache size, the factor of decrease needed to turn the misses into hits increases!

3. Bringing reuses closer together means removing data accesses from between use and reuse.

4. Map the intermediate data accesses at run-time to the corresponding static source code.

To be able to eliminate the data accesses between distant reuses, one needs to know the source code that produced those accesses. Therefore, the code executed between reuses is measured by SLO.

5. Find the highest level in the call-loop tree that is executed between use and reuse.

Bringing the reuses closer together requires a refactoring of the source code executed between use and reuse, in such a way that the reuses may be drastically moved closer together. Finding an appropriate refactoring to accomplish this proceeds by analyzing the function calls and loop structure that is executed between use and reuse. Conceptually, SLO builds the hierarchy of all loop iterations, loop executions and function calls. By identifying the highest level where iteration, loop or function call boundaries are crossed, an appropriate code refactoring is pinpointed. An example may make this a bit clearer:

Above, the call-loop hierarchy of the running program is indicated.

There are three types of levels in the loop hierarchy:

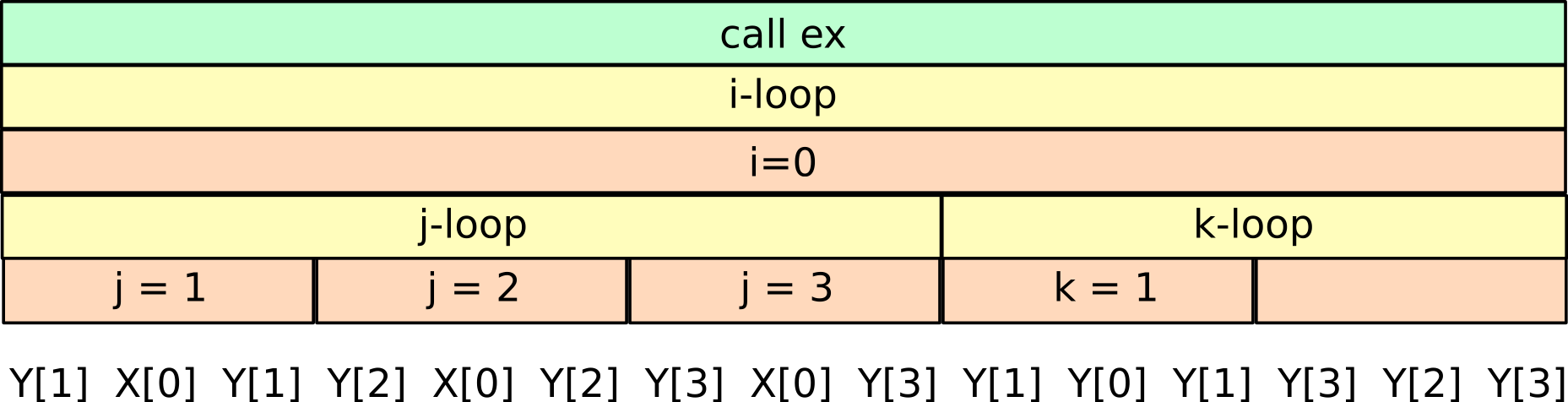
iteration-level indicates the execution of a single loop iteration at run-time.
loop-level indicates the execution all iterations of a complete loop at run-time.
function-level indicates the execution of a function at run-time.

6. Based on the kind of level, apply the appropriate refactoring, that may bring reuses subtantially closer together.

Depending on whether reuses occur between different iterations, different loop executions or different calls, a different refactoring is required to bring reuses closer together. The following refactorings are indicated by SLO, depending on the highest-level in the function-loop hierarchy that is crossed between use and reuse.

iteration-level: since reuses occur between iterations of the same loop, less data must be accessed in a given iteration of the loop to reduce the reuse distance. Some kind of LOOP TILING is needed.
loop-level: when the use occurs in one loop, and the reuse in another loop, it means the both loops iterate over the same data. Instead of traversing the same data twice, the computations in both loop should be performed in a single traversal of the data. This can be accomplished by LOOP FUSION.
function-level: when the use occurs in one function, and the reuse in another function, it means both functions perform computations on the same data. The computations in both functions should be merged, so that a single traversal of the corresponding data structure results. Therefore, some kind of FUNCTION FUSION is needed.

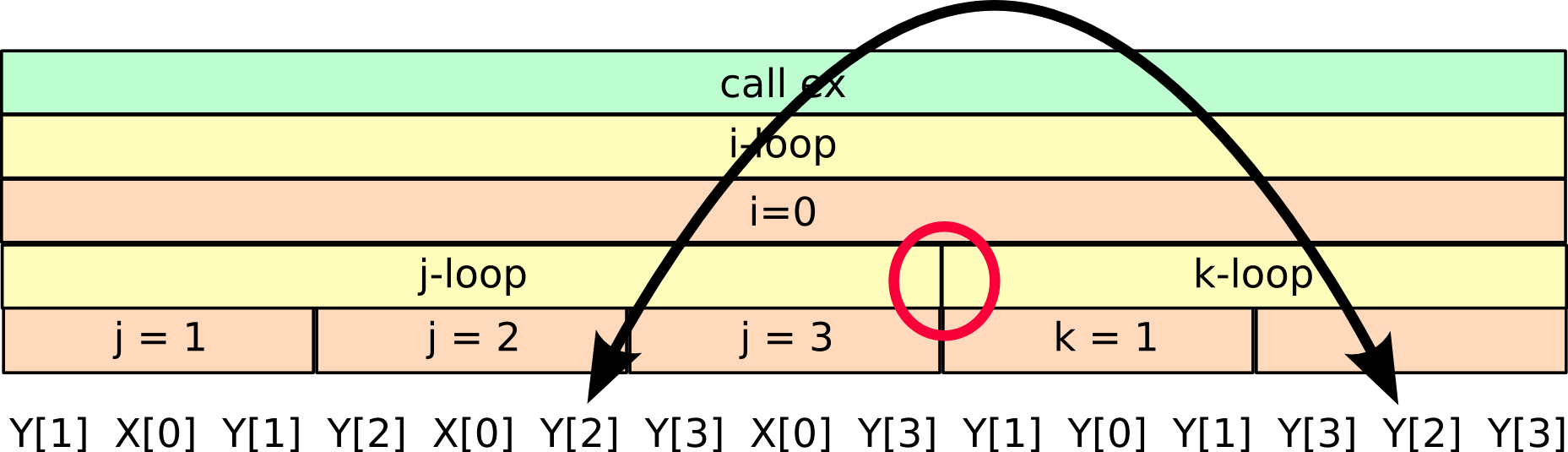
Above, the call-loop hierarchy of the running program is indicated. Since for the indicated reuses, the highest-level crossed in the function-loop hierarchy is at the loop-level, the corresponding loops should be fused to increase the locality of that reuse. I.e. loops j and k should be fused.

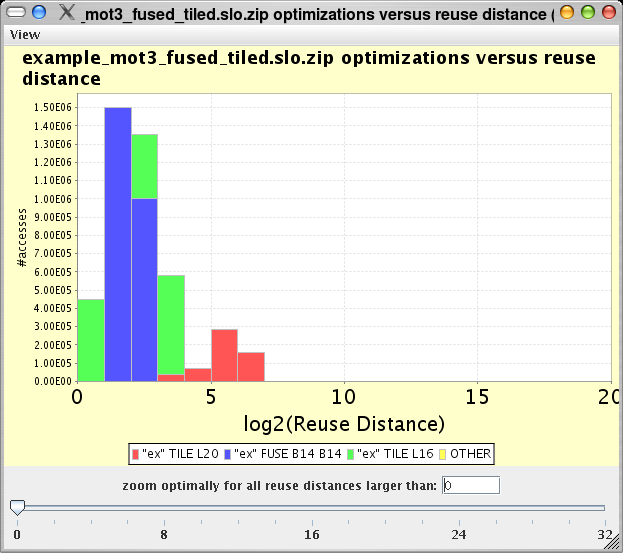
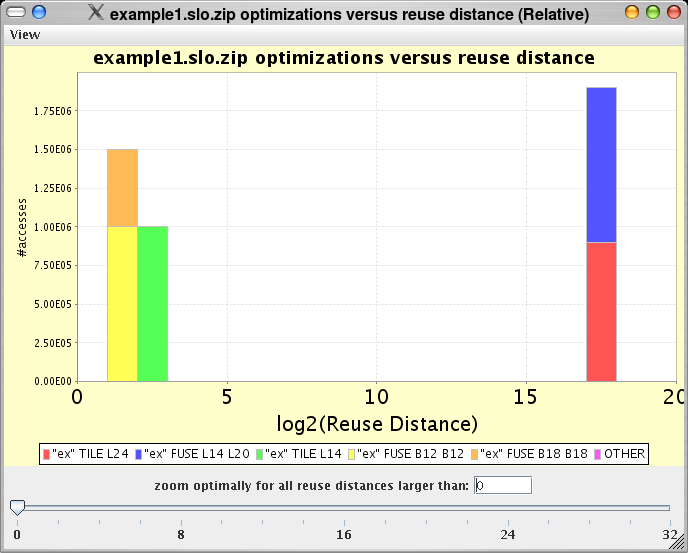
For the running example, SLO shows the following histogram of reuse distances. Each color indicates a different refactoring as found by the analysis described above. As can be seen from the histogram, two different refactorings are required to optimize the long-distance reuses (the blue and the red optimization).

After clicking on the blue optimization, SLO indicates the blue refactoring as follows in the source code:

It shows that both loops should be fused. The red optimization requires tiling the outer loop, as shown in the following screenshot:

After applying these optimizations, the code looks as follows:

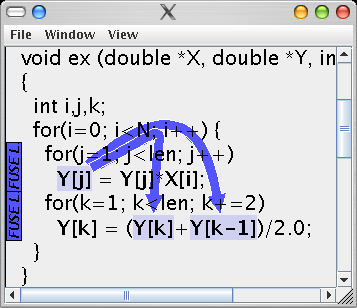
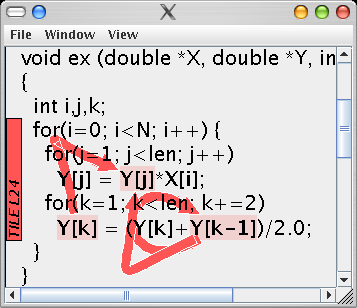
The histogram of reuse distances show that all long reuse distances have been shortened drastically:

As a result, the program runs faster. E.g. on a 2.66Ghz Pentium4, the program runs more than 5 times faster.